Où la physique en est-elle du déterminisme ?

Les lois qui gouvernent le monde naturel, celles de la physique, soutiennent-elles l’idée que le futur est déjà écrit ? C’est ce qu’on appelle le problème du déterminisme en physique. Cette question n’est pas sans intérêt pour nous car souvent connectée à celles du libre arbitre, de la prescience de Dieu, ou de la prédestination. Par exemple, dans son ouvrage The Reformed Doctrine of Predestination rédigé en 1932^[1], le théologien Américain Loraine Boettner citait le déterminisme du monde physique à l’appui de la théologie de la prédestination.

Il se trouve que le statut scientifique du déterminisme a pas mal évolué depuis un siècle. Partant de la physique du XIX siècle qui soutenait le déterminisme le plus strict, la mécanique quantique, la relativité, puis la théorie du chaos sont passées par là, qui ont pas mal changé les choses. J’aimerais dans cet article retracer brièvement l’évolution du déterminisme en physique pour voir où nous en sommes aujourd’hui.

L’apport de la relativité est discuté juste avant la conclusion, et peut se lire indépendamment du reste. Pour ceux qui ont l’habitude de jeter un œil à la fin des romans policiers avant de les avoir terminés, voici la conclusion : je crains fort que la réponse de la physique actuelle à la question du déterminisme ne soit digne du meilleur Normand. Pour ceux qui voudraient comprendre comment on arrive là, on y va !

La mécanique classique, au XIX siècle

ommençons par revenir 200 ans en arrière,
et écoutons ce que Pierre Simon de Laplace (1749-1827),
l’un des plus grands scientifiques de son temps,
avait à dire à cet époque :

Une intelligence qui, à un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d’ailleurs elle était suffisamment vaste pour soumettre ces données à l’analyse, embrasserait dans la même formule les mouvements des plus grands corps de l’univers et ceux du plus léger atome ; rien ne serait incertain pour elle, et l’avenir, comme le passé, serait présent à ses yeux.

– Pierre Simon Laplace, Essai philosophique sur les probabilités, 1814

Telle était la situation en ce début de XIXe siècle. Selon les lois de la nature connues à l’époque, le déterminisme ne faisait aucun doute. Donnez-moi la position et la vitesse de tous les objets de l’univers à ce même instant. Ce qu’on appelle les « conditions initiales ». Puis donnez-moi la façon dont ces objets interagissent entre eux : les maths me permettent d’en déduire l’évolution future (et passée) de tous ce beau monde depuis maintenant, jusqu’à l’infini. En bref,

Conditions initiales + équations du mouvement = futur déjà déterminé.

Notons que l’impossibilité pratique de connaitre la position et la vitesse de tous les objets de l’univers n’entre pas du tout en ligne de compte. Ce qui compte, pour un physicien du début du XIXe siècle, c’est que ces données existent. Si de plus on connait la loi d’interaction entre les objets en question, les maths font le reste du travail. Ces dernières vous assurent que le couple « conditions initiales + lois du mouvement » produit une évolution unique dans le futur^[2]. Notons que les maths vous assurent que cette évolution existe, sans pour autant vous dire systématiquement à quoi elle ressemble. En tout état de cause, le futur n’apporte rien de neuf. Tout est écrit, même quand personne ne peut le lire.

Mais de l’eau a coulé sous les ponts des physiciens depuis 200 ans. La mécanique quantique, la relativité, la théorie du chaos sont passées par là. Où en est-ont en ce début du XXIe siècle ? Les lois de la physique connues à ce jour nous dévoilent-elles encore un futur sans surprise ?

L’apport de la mécanique quantique

a mécanique quantique (MQ) a révolutionné la description du monde à l’échelle microscopique. Les gens se sont rendus compte, par exemple, qu’un électron qui « tourne » autour d’un proton ne se comporte pas du tout comme une petite bille tournant autour d’une autre, en se soumettant aux lois de la physique connue au XIXe siècle.

Bien qu’elles ne constituent pas le cœur de l’article, deux petites remarques en passant :

• J’ai mis des guillemets autour de « tourne » car justement, la description quantique de l’électron ne permet plus de lui attribuer ce genre de mouvement.
• Il est fréquent que l’aspect quantique microscopique montre son nez au niveau macroscopique, c’est-à-dire au nôtre. Par exemple, le comportement des électrons dans un bout de métal à température ambiante est incompréhensible sans la MQ.

Mais revenons à nos moutons. Indépendamment de son côté peu intuitif, cette MQ décrit-elle encore l’évolution des particules avec des équations mathématiques, comme le faisait la physique de Laplace ? Oui. Et ces équations mathématiques, ont elles une solution unique une fois les conditions initiales données, comme c’était le cas pour la physique de Laplace ? Re-oui. Où est le problème, alors ? Pourquoi dit-on que la MQ remet en cause le déterminisme ? On y vient.

Selon la MQ, l’évolution d’un électron dans une expérience donnée est parfaitement déterministe. Mais un jour ou l’autre, il faut bien faire une mesure pour vérifier tout cela. Et c’est là qu’est l’os : le résultat de la mesure n’est pas déterministe. Prenons une célèbre expérience pour exemple, celle de Stern et Gerlach : on fait passer des électrons dans un champ magnétique. Les équations de la MQ qui déterminent ce qu’ils vont faire sont tout à fait déterministes. Maintenant, quand on essaye de mesurer l’endroit où arrivent les électrons après avoir traversé le champ, on ne trouve que deux endroits. Pas plus. Les lois de la MQ peuvent tout à fait vous dire quels sont ces deux endroits. Mais elles ne peuvent pas vous dire où votre électrons va finir. Elles ne vous donnent qu’une probabilité. Dans ce cas, c’est 50/50.

Vous pouvez faire exactement la même expérience deux fois de suite, et mesurer un électron « en haut » pour la première, et « en bas » pour la seconde. L’incertitude est intrinsèque. Elle n’a rien à voir avec la façon dont on a lancé l’électron, comment il était au début, etc. La même cause ne produit pas le même effet. Trois questions ont fait (et font) couler beaucoup, beaucoup, beaucoup d’encre :

• Les équations de la MQ prédisent un nombre infini de configurations pour l’électron après son passage dans le champ, tant qu’on ne l’a pas mesuré^[3]. Comment se fait-il que seules 2 puissent être le résultat d’une mesure ? La question ici n’est pas le nombre 2 en soi. Quand on met les mains dans le cambouis mathématique, on comprend très bien d’où vient ce 2 (ou bien 3, ou 4, ou que sais-je, dans d’autres expériences). La question est : pourquoi diantre ne puis-je pas mesurer autre chose ? C’est la question connue sous le doux nom de « réduction du paquet d’onde ».
• OK, admettons que je ne puisse mesure que 2 résultats. Mais n’y aurait-il pas moyen de savoir lequel va sortir ? L’impossibilité pour la MQ de donner autre chose que des probabilités ne serait-elle pas le fruit d’une incomplétude de cette dernière ? Peut-être que dans 200 ans, on trouvera l’ingrédient qui manquait, et qui permettra de prédire avec certitude LE résultat de la mesure ? C’est ce que l’on a appelé la possible existence de « variables cachées ». C’est aussi le célèbre « Dieu ne joue pas aux dés » d’Einstein, qui n’admettait pas que la nature puisse être fondamentalement probabiliste. Non-déterministe.
• D’accord, mon électron ne peut être correctement décrit que par la MQ. Mais le monde que je vois autour de moi marche comme celui de Laplace. Il semble déterministe. Où donc est la frontière entre ce monde « classique », que j’expérimente tous les jours, et le monde quantique ? Combien faut-il empiler d’électrons pour qu’ils arrêtent de faire des bêtises quantiques ?

Le premier point a donné lieu à toutes sortes d’interprétations ainsi qu’à nombre d’envolées liriquo-mystiques^[4]. Il semble en fait que cette réduction du nombre de mesures possibles est le fruit mathématique de l’interaction du système quantique avec un environnement fait d’un très grand nombre d’atomes… comme un appareil de mesure et un laborantin. On appelle cela « décohérence quantique ». En d’autres termes, les mêmes équations de la MQ vous donnent un nombre de configurations infini pour un électron isolé du reste du monde, mais deux seulement pour un électron en contact avec le reste du monde (dans l’expérience de Stern et Gerlach). Et pour le mesurer, il faut bien le mettre en contact avec le reste du monde.

Le second point continue de faire parler de lui. Il fut en son temps le centre d’un titanesque débat scientifique entre Einstein et Bohr. Dieu joue-t-il aux dés ? Aujourd’hui, après un siècle de mécanique quantique, après des millions d’expériences satisfaisantes^[5], après des tests expérimentaux sans fin, après des prédictions d’une précision inouïes^[6], équivalentes à prévoir la distance Los Angeles-Sydney à moins d’un cheveu près, la réponse est « oui ». Il ne manque aucun ingrédient à la MQ. Le monde microscopique semble fondamentalement indéterministe. Les mêmes causes ne produisent pas toujours les mêmes effets. Tout indique que « Dieu joue aux dés »^[7].

Enfin, le dernier point, la frontière classique-quantique, n’est pas en reste. Il est toujours le sujet d’intenses recherches, souvent en liaison avec la décohérence quantique évoquée plus haut. Le dernier prix Nobel de Physique Français, Serge Haroche, est passé maître dans l’art de concevoir des expériences pour observer la frontière en question. Je laisse au lecteur le plaisir de visiter sa page du Collège de France pour en savoir plus.

Faisons l’état des lieux après le passage de la MQ. Le monde macroscopique, celui de Laplace, fait d’un très grand nombre d’atomes, est régit par des lois déterministes. Ça, ça tient toujours. Mais le monde microscopique est affligé d’un indéterminisme fondamental. La paroi est-elle étanche entre les deux ? C’est là que la théorie du chaos entre en jeu.

L’apport de la théorie du chaos – Acte 1

 ce stade, on pourrait penser que certes, le monde microscopie est indéterministe. Certes, la MQ ne donne que des probabilités, et on ne peut rien espérer de mieux. Mais n’importe quel objet est fait d’un nombre immense^[8] d’atomes régis par la MQ. Et quand on les applique à des nombres immenses, les probabilités se transforment en certitudes. Toute la thermodynamique est fondée là-dessus, le second principe de la thermodynamique, n’échappe pas à la règle.

Bref, on pourrait penser que l’indéterminisme au niveau microscopique… y reste. Ce ne sont pas des atomes individuels qui dirigent le monde, mais des ensembles d’un nombre inouï d’atomes. Et pour ces ensembles, les probabilités se transforment en certitudes.

Mais en fait, non. Le microscopique peut tout à fait pointer son nez au niveau macroscopique. Sans même parler de théorie du chaos, on peut imaginer deux laborantins qui parieraient une tournée sur le résultat d’une mesure quantique. Dans ce cas, c’est l’indéterminisme quantique de la mesure qui décide en fin de compte de celui qui payera la tournée au bar du coin. Le destin d’un électron isolé a bel et bien influencé le cours du monde de monsieur-tout-le-monde.

Mais trêve de scénarios alambiqués, posons-nous la question : si l’indéterminisme de la MQ peut changer, ne serait-ce que de manière infime, les conditions initiales du monde de Laplace, à quelles conséquences peut-on s’attendre ? On pourrait en fait imaginer deux scénarios :

• Si les conditions initiales changent un tout petit peu, l’évolution future du système ne change pas. Ou presque pas. Ici, l’indéterminisme microscopique n’a pas d’influence sur le monde macroscopique. Ce dernier reste déterministe, « à la Laplace ».
• Si les conditions initiales changent un tout petit peu, l’évolution future du système peut changer radicalement. Ici, l’indéterminisme microscopique contamine le monde macroscopique. Ce dernier n’est donc plus déterministe.

Ce que la théorie du chaos a montré, c’est que le deuxième cas de figure est en fait très fréquent. Le savait-on depuis longtemps ? Oui et non. Oui, car on savait depuis longtemps que si une goutte d’eau tombe sur mon toit, elle va finir du côté droit de ma maison si elle tombe un tout petit peu à droite du faîte, et à gauche de ma maison, si elle tombe ne serait-ce qu’un millimètre à gauche du faîte. Petite différence au départ, grande différence à l’arrivée.

Non, car ce qu’on ne savait pas, disons avant les années 60, c’est que ce genre de situation est très répandue. Pourquoi a-t-il fallu attendre les années 60 ? Parce qu’à l’exception de cas très simples, les équations du monde de Laplace ne peuvent généralement pas se résoudre « à la main », avec un papier et un crayon. Pour voir à quoi ressemblent les solutions, il faut un ordinateur.

C’est ainsi qu’en 1961, Edward Lorentz, qui s’amusait à résoudre un système d’équations « à la Laplace », remarqua que l’ordinateur lui donnait une évolution complètement différente suivant que l’une des conditions initiales était 0,506 au lieu de 0,506127. Il venait de découvrir le célèbre effet papillon. Et la chose a été abondement confirmée, étudiée, disséquée, depuis. Dans certains cas, une infime variation des conditions initiales provoque une évolution complément différente au bout d’un certain temps.

Faisons le point : notre monde macroscopique, le « monde de Laplace », est régit par des lois complétement déterministes. Vous leur donnez les conditions initiales, et elles vous déroulent le futur. Mais le monde microscopique, lui, obéit à la MQ. Il est l’objet d’un indéterminisme intrinsèque, fondamental, irréductible. On peut dont imaginer, par exemple, que les conditions initiales des équations de Laplace^[9] sont susceptibles de varier de façon fondamentalement imprévisible. Infime, certes, car émanant de l’échelle atomique, mais imprévisible quand même. Pour finir, cerise sur le gâteau, la théorie du chaos vous assure que ces infimes variations des conditions initiales peuvent se voir amplifiées de manière disproportionnée. Une série de conditions initiales vous donnent un « futur de Laplace ». Une autre, pourtant infiniment voisine, vous en donne un autre totalement différent.

Le déterminisme est-il mort ? Plus précisément, la physique actuelle l’a-t-elle abandonné? Peut-être pas. Et curieusement, encore à cause de la théorie du chaos.

L’apport de la théorie du chaos – Acte 2

u-delà de l’extrême sensibilité aux conditions initiales
dont nous venons de parler, les gens qui se sont mis à étudier
la théorie du chaos vers le milieu des années 60
se sont rendus compte de quelque chose de très intéressant^[10].

Ils ont découvert l’existence des attracteurs.

Certes, les histoires peuvent diverger rapidement pour des conditions initiales peu différentes. Mais il ne se passe pas n’importe quoi pour autant. On s’est rendu compte que dans pas mal de cas, les histoires présentent des points communs relativement insensibles aux conditions initiales.

Premier exemple : L’atmosphère terrestre est un système très compliqué, tout à fait. Pourtant, les anticyclones ou les dépressions que nous montre la météo se ressemblent tous plus ou moins. Ils ont toujours plus ou moins la même taille, tournent dans le même sens, manifestent des pressions comparables, etc.

Deuxième exemple : les océans forment eux aussi un système hautement complexe. Pourtant, il existe au niveau mondiale un réseau de courants marins maintenant bien connus, et stables. C’est compliqué, mais il ne se passe pas n’importe quoi pour autant.

La notion d’attracteur est aussi utilisée en biologie, par exemple dans les recherches visant à comprendre la morphogenèse. Comment un ensemble de cellules en interaction finit-il par former une feuille, ou une branche ? Les conditions initiales ne peuvent pas être exactement toujours les mêmes. Pourtant, toutes les feuilles d’un même arbre se ressemblent plus ou moins. Il est probable (je ne sais pas si c’est démontré) que la forme finale est un attracteur du système^[11].

Un attracteur n’est pas toujours une forme identifiable dans l’espace habituel. Dans la plupart des cas, c’est une structure tout à fait identifiable, certes, mais dans un espace mathématique assez abstrait. Ce qui en revanche ne change pas, c’est que l’on voit les trajectoires s’enrouler autour de la structure en question. Ou bien osciller autour. Ou bien s’en rapprocher de plus en plus. Comme si la structure en question les attirait, d’où son nom d’ « attracteur ».

Un même système d’équations « genre Laplace » peut avoir plusieurs attracteurs. Si on choisit telles ou telles conditions initiales, on s’enroule autour de l’attracteur A. Pour d’autres conditions initiales, on aboutit à l’attracteur B. Ainsi de suite. L’ensemble des conditions initiales qui mènent au même attracteur est très justement nommé le « bassin » de l’attracteur en question. Exactement comme le bassin de la Seine est par définition la partie du territoire où toute l’eau qui tombe finit dans la Seine.

Je pense que vous aurez deviné ou je veux en venir : l’existence des attracteurs tempère l’anarchie véhiculée par l’extrême sensibilité aux conditions initiales. Des trajectoires initialement très voisines peuvent diverger énormément, certes. Mais si notre système admet un attracteur (ce n’est pas obligé), deux trajectoires dont le point de départ est dans le même bassin finiront autour du même attracteur, de la même manière que la pluie qui tombe à Rouen, Paris ou Troyes finit de toute façon dans la Seine, puis au Havre. On retrouve finalement une sorte de déterminisme « mou ». Tant qu’on ne change pas de bassin d’attracteur, les trajectoires auront des points communs, et ce, aussi loin que l’on regarde dans le temps. On change de futur, mais pas radicalement.

L’apport de la relativité

ême si le développement de la relativité
est contemporain de celui
de la Mécanique Quantique,
voire même antérieur^[12],
j’ai choisi de traiter en dernier son apport
au problème du déterminisme.

Si en effet les contributions de la mécanique classique, puis de la théorie quantique et enfin de celle du chaos, forment un tout relativement cohérent (j’espère que ça s’est vu), celle de la relativité semble faire cavalier seul.

Je vais donc parachuter, sans expliquer son origine, un surprenant résultat de relativité. Qu’on sache tout de même que jamais, depuis 100 ans, elle n’a été mise expérimentalement en défaut. Sans elle, les GPS du monde entier n’auraient qu’une précision de 1 km. Sa formule de dilatation du temps a récemment été testée expérimentalement avec une précision de 2 pour 1 milliard^[13], ce qui revient à prédire la distance Paris-New York à 1 centimètre près^[14]. Bref, pour bizarroïde que paraisse ce que vous êtes sur le point de lire, on est en terrain extrêmement sûr.

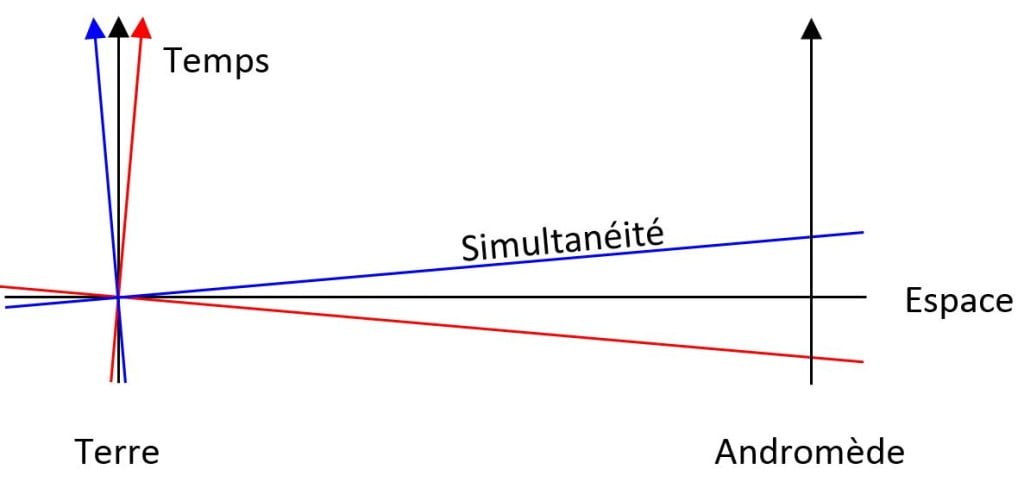
Imaginons pour simplifier que l’espace ait 1 seule dimension. On peut ainsi représenter l’espace-temps dans un diagramme à deux dimensions, comme dans la figure ci-dessous (ne regardez que les trais noirs pour le moment). Imaginons deux personnes, Alice et Bob, ensemble, sur terre, et un extra-terrestre du nom de Xyzlkf^[15] dans la galaxie d’Andromède. Tous sont immobiles les uns par rapport aux autres. Alors la ligne horizontale noire définit « l’espace de simultanéité » de ces 3 personnes. Leur présent. Leur « maintenant ». L’ensemble des évènements qui se passe « en même temps ».

Supposons que Alice se rapproche d’Andromède en marchant, à disons 4 km/h. Et bien selon la relativité, son espace de simultanéité est maintenant représenté par la ligne bleue, qui coupe l’axe temporel d’Andromède environ 4 jours plus tard ! Et si Bob s’éloigne d’Andromède à 4 km/h, son « maintenant » est représenté par la ligne rouge, qui coupe l’axe temporel sur Andromède environ 4 jours plus tôt.

Où donc est le problème ? Et bien selon que l’on s’éloigne ou que l’on se rapproche d’Andromède à seulement 4 km/h, l’espace de simultanéité là-bas bouge dans le temps de plus ou moins 4 jours. En d’autres termes, la réponse à la question « quelle jour est-on en ce moment même, sur Andromède » dépends de ma vitesse de déplacement. Supposons que l’on soit dimanche sur terre. Pour Alice qui se rapproche, la réponse est « jeudi ». Pour Bob qui s’éloigne, la réponse est « mercredi ».

Comme l’indique la figure, plus on est loin, plus l’effet est marqué. Mais si la distance à Andromède vous gêne, sachez qu’on peut tout à fait obtenir le même effet en pensant à la Lune, ou même à la pièce d’à côté. Seulement, il faut aller beaucoup plus vite. La formule permet un déplacement temporel arbitrairement grand, pour une distance arbitrairement petite. L’intérêt de prendre Andromède est qu’on obtient un décalage temporel de plusieurs jours en se contentant de marcher.

Quel rapport avec le déterminisme ? Et bien si n’importe quel moment du futur sur Andromède peut appartenir à mon « présent » pour une vitesse de déplacement convenablement choisie, c’est que ce moment existe déjà. Tel est le raisonnement. Inversement, si en se déplaçant à une vitesse bien choisie, mon copain extra-terrestre Xyzlkf sur Andromède peut devenir contemporain, entrer en simultanéité avec n’importe quel moment de mon futur, c’est que mon futur existe déjà.

L’argument est connu sous plusieurs noms. Celui de Rietdijk–Putnam, par exemple, du nom des deux scientifiques qui l’ont énoncé pour la première fois. Notons que le titre de l’article de Rietdijk était « Une preuve rigoureuse du déterminisme dérivée de la théorie de la relativité »^[16], ce qui est tout de même assez explicite. C’est le physicien anglais Roger Penrose qui s’est amusé à impliquer Andromède dans l’histoire à cause de la distance énorme mise en jeu, qui permet de se contenter d’une marche à pied pour obtenir des jours de différence^[17].

L’univers parfaitement déterministe dont accouche ce raisonnement est parfois appelé « univers bloc ». Le futur existe déjà, de la même manière que la fin d’un film existe déjà même si vous n’en êtes qu’au début.

Alors, est-on en présence d’une authentique preuve du déterminisme ? L’affaire est-elle entendue, et fait-elle l’objet d’un large consensus scientifique ? Il semble que non. En fait, les physiciens sont partagés. Certains, comme Brian Greene, sont convaincus. Il en parle abondamment dans son livre La Magie du Cosmos^[18], et l’illustre très bien dans cette vidéo. De l’autre côté, l’une des objections que l’on oppose à l’univers-bloc est qu’il ne rend pas compte du passage du temps. Pourquoi le temps passe-t-il ? Et pourquoi à cette vitesse, et dans ce sens ?

On va s’arrêter là car ça commence à faire pas mal. Le lecteur intéressé peut visiter la page Wikipédia en lien à partir du terme « univers bloc » ci-dessus. Quoi qu’il en soit, les questions que soulève cette histoire d’univers bloc sont si profondes et complexes qu’un consensus n’a pas eu le temps de s’installer et ne le fera peut-être jamais.

Conclusion

i l’espace-temps est un bloc, comme le suggère le raisonnement de la section précédente, alors l’affaire est entendue. Nous sommes revenus au déterminisme du XIXe siècle. Dans ce cas, la mécanique quantique, le chaos et tout le toutim n’ont plus qu’à se débrouiller pour accoucher d’un tel déterminisme, même si on ne sait pas comment ils pourraient faire. Hélas (pour ceux qui auraient espéré une réponse tranchée), il n’y a pas de consensus scientifique sur l’univers bloc. L’hypothèse constitue en tous cas un formidable générateur de questions passionnantes.

Tournons-nous maintenant uniquement vers le tandem « mécanique quantique-théorie du chaos ». Ici, le déterminisme « dur » de Laplace ne semble plus du tout soutenu par ce que l’on sait des lois de la physique. Des évènements intrinsèquement aléatoires à l’échelle microscopique peuvent influencer le monde macroscopique, si bien qu’une intelligence qui, à un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent (paraphrasons Laplace), ne connaitraient pas pour autant l’avenir avec certitude. Mais pourrait-il le connaitre, dans les grandes lignes ?

Même si le déterminisme qui subsiste ne peut être que « mou » (on ne change pas de bassin d’attracteur), plusieurs questions subsistent qui risquent de rester ouvertes pour toujours :

1. L’univers dans son ensemble a-t-il un attracteur ? Si l’on pouvait écrire le système d’équations décrivant l’évolution de tout l’univers, lui découvrirait-on un attracteur ?
   S’il n’en a pas, alors la sensibilité aux conditions initiales n’a rien pour la tempérer. La moindre fluctuation quantique change le futur.
2. Supposons maintenant que l’univers possède un ou plusieurs attracteurs. Tout dépend alors de la manière dont leurs bassins sont arrangés les uns par rapport aux autres. S’ils sont positionnés tels les bassins des fleuves que nous connaissons, c’est que tant que l’on est bien dedans, on ne risque pas d’en sortir en remuant un peu. Déterminisme mou, donc. Mais si l’on passe tout près de la frontière entre deux bassins, alors une pichenette quantique peut vous faire basculer dans un autre bassin. Indéterminisme total.
   Enfin, il est des cas où les basins sont intriqués. Intimement entrelacés, de sorte qu’autour de n’importe cercle, si petit soit-il, tracés autour d’un point d’un bassin, on trouvera nécessairement des points d’un autre bassin^[19]. Ici, de nouveau, indéterminisme. La moindre fluctuation quantique vous fait sauter de bassin, et il n’existe pas de refuge. Pas d’endroit d’où l’on puisse faire un pas à gauche ou à droite sans risque de changer de bassin.

Bien qu’il s’avère passionnant de retourner ces deux questions dans tous les sens, je doute fort que la physique puisse un jour leur donner une réponse définitive. Comment donc analyser les attracteurs du système dynamique « univers entier », ainsi que leurs bassins ?

Résumons pour finir : la physique du XIXe siècle est complètement déterministe. Conditions initiales + équations = futur déterminé de manière unique. Puis la vient la Mécanique Quantique, qui introduit un élément de hasard intrinsèque au niveau des conditions initiales. S’y ajoute la théorie du chaos qui nous enseigne qu’une minuscule fluctuation des conditions initiales peut tout à fait accoucher d’un futur complètement différent.

A ce stade, on pourrait conclure que la physique actuelle ne soutient plus du tout le déterminisme façon Laplace. Elle l’a éparpillé façon puzzle. Reste la possibilité, probablement insondable, d’un déterminisme mou reposant sur l’espoir que les bassins des attracteurs de l’univers ne soient pas trop exotiques. Enfin, il est possible que l’espace-temps soit un bloc existant déjà. On retombe alors sur le déterminisme de Laplace, et la question à 100 euros devient « comment le couple mécanique quantique-théorie du chaos, qui au mieux nous donne un déterminisme mou, fait-il pour accoucher d’un univers parfaitement déterministe ?»

Tout cela pour dire que si on la convie au débat millénaire sur le libre arbitre, la physique actuelle risque fort de n’apporter qu’une réponse de Normand : Pt’et bien qu’oui, pt’et ben qu’non.

Notes

^[1] The Reformed Doctrine of Predestination, Loraine Boettner, ch. 25.

^[2] Les équations du mouvement ne font apparaitre que la vitesse, la position, et l’accélération des objets. Et un superbe théorème de maths vous assure de l’existence d’une solution unique à ce genre d’équations, une fois que les vitesses et les positions initiales ont été données.

^[3] Avant la mesure, il peut être dans n’importe quelle superposition des deux états que l’on peut mesurer. La MQ décrit l’évolution de cette superposition de manière complètement déterministe.

^[4] Il suffit de taper “mécanique quantique et parapsychologie” dans Google pour en ramener un camion.

^[5] Chaque micro-processeur est une expérience ambulante de mécanique quantique. Je vous laisse compter.

^[6] Theorie: T. Aoyama, et al. Tenth-Order QED Contribution to the Electron g-2 and an Improved

Value of the Fine Structure Constant. Physical Review Letters, 109:111807, 2012.

Experience: D. Hanneke, et al. New measurement of the electron magnetic moment and the fine

structure constant. Physical Review Letters, 100:120801, 2008.

^[7] Voir la page Wikipédia sur le problème des Variables Cachées pour en savoir plus.

^[8] Du genre, cent mille milliards de milliards. Un « 1 » suivi de 23 zéros, noté 10²³. Avec 10²³ kilomètres, on arrive à la plus lointaine galaxie connue (environ 13 milliards d’années-lumière). Mais avec 10²³ molécules d’eau (H₂O), on fait juste un petit verre d’eau de 18 ml.

^[9] Ce ne sont pas celles de Laplace, plutôt de Newton. Mais on se comprend.

^[10] James Gleick raconte tout cela très bien dans son livre La théorie du chaos.

^[11] Voir par exemple Morphogenesis: Origins of Patterns and Shapes, Paul Bourgine, Annick Lesne, Springer Science & Business Media, 2010.

^[12] La relativité restreinte date de 1905. La générale de 1915. L’équation de Schrödinger de 1925.

^[13] Test of Time Dilation Using Stored Li+ Ions as Clocks at Relativistic Speed, Physical Review Letters 113, 120405 (2014).

^[14] Ce n’est pas que la relativité s’est trompée de 1 cm. C’est que la mesure expérimentale n’avait qu’une précision équivalente à 1 centimètre.

^[15] Comme chez Gotlib. C’est pas un faute de frappe.

^[16] Rietdijk, C.W. (1966) A Rigorous Proof of Determinism Derived from the Special Theory of Relativity, Philosophy of Science, 33 (1966) pp. 341–344

Putnam, H. (1967). Time and Physical Geometry, Journal of Philosophy, 64, (1967) pp. 240–247

^[17] Roger Penrose, L’esprit, l’ordinateur et les lois de la physique, Dunod, 1993, p. 217.

^[18] Brian Greene, La Magie du Cosmos, ch 3 & 5.

^[19] On trouve par exemple des structures de type fractal.