Par Antoine Bret – Physicien chercheur
Mise en jambe
Prenez un pendule, un poids, assez lourd, au bout d’une longue corde. Vous l’écartez franchement de la position verticale, puis vous le lâchez. Il s’éloigne de vous, repasse par la position verticale, puis continue sur sa lancée. Ayant atteint son point le plus haut de l’autre côté de la pièce, il s’arrête et repart en sens inverse pour revenir vers vous.
Si l’expérience se déroule dans une pièce où l’on a enlevé tout l’air, presque aucun frottement ne viendra amortir le mouvement, et le pendule va osciller très longtemps. Mais comme il n’est pas facile de faire le vide dans la plupart des endroits, on se contentera d’un très long pendule.
Tant que rien ne vient perturber le mouvement et que vous ne bougez pas, le pendule devrait osciller dans le plan vertical qui passe entre vos deux yeux. Pourtant, si vous attendez un peu, vous verrez que le plan dans lequel oscille le pendule tourne lentement. La bonne vieille loi de Newton « Force = masse x accélération » serait donc fausse ? Elle prédit en effet que le plan d’oscillation du pendule ne devrait pas tourner alors que vous, vous le voyez tourner. C’est la fameuse expérience du pendule de Foucault, que fait tourner la fameuse force de Coriolis[1].
Et bien oui, la loi de Newton est fausse… dans votre référentiel. Existe-t-il un référentiel dans lequel elle soit vraie ? Demandez au pendule : si vous avez initialement lâché le pendule en direction du soleil, vous verrez qu’il tourne de telle sorte qu’il continue de montrer le soleil. De fait, il accomplira un tour complet en exactement 24 heures.
Tous les référentiels ne se valent pas (même si on entend très souvent le contraire). Même dans une pièce fermée sans communication avec l’extérieur, la rotation du pendule vous indique que vous être en train de vous repérer par rapport à un référentiel dans lequel la loi de Newton est fausse. Si maintenant vous oubliez ce que le pendule fait par rapport à la pièce pour vous concentrer sur sa trajectoire par rapport au soleil, vous pouvez décrire son mouvement par la loi de Newton.
Pour la petite histoire, les référentiels dans lesquels la loi de Newton marche sont dits « inertiels » ou « galiléens ».[2] Le point de départ de la relativité restreinte d’Einstein, c’est que les lois de la nature sont les mêmes dans tous les référentiels inertiels.
Mais revenons au pendule. Sa rotation par rapport à la terre, mais pas par rapport au soleil, vous indique donc que la terre tourne sur elle-même. Serait-il possible que ce soit le contraire ? Certains prétendent que la déviation du pendule pourrait s’expliquer si la terre était fixe[3], tandis que le reste de l’univers tournerait autour. Ils s’appuient en cela sur un calcul montrant que selon la théorie de la relativité générale, un pendule placé au centre d’une coquille en rotation serait soumis à une force type Coriolis. La coquille entraînerait l’espace-temps avec elle. Bref, il tournerait, genre pendule de Foucault (effet Lense–Thirring). On peut objecter à cela que :
- Selon l’effet en question, le pendule ne fait pas un tour entier chaque fois que la coquille en fait un. La masse en rotation se contente d’entrainer le pendule (d’où le terme « frame-dragging » en anglais). Entre 2004 et 2010, la NASA a testé avec succès cet effet sur un gyroscope en orbite (Gravity Probe B). L’objet en rotation censé « entrainer » l’espace-temps autour de lui était la terre. Le satellite faisait le tour de la terre en 1h38. Si le gyroscope avait fait un tour entier toutes les 98 minutes, la NASA n’aurait pas eu à dépenser 750 millions de dollars pour en mesurer la rotation.[4]
- L’extension de l’effet à l’univers entier pose des problèmes théoriques qui divisent encore les experts[5].
- Le raisonnent ne singularise en rien la terre. On peut tenir exactement le même pour tous corps en rotation par rapport au reste de l’univers. Depuis la toupie de votre enfant jusqu’au soleil ou n’importe quelle étoile, en passant par des milliers de planètes[6].
Imaginons néanmoins que la terre soit fixe[7] et que le reste de l’univers tourne autour en 24 heures. Voici un certain nombre de conséquences qui montrent l’impossibilité de la chose.
Les satellites géostationnaires tomberaient
Un satellite géostationnaire est en orbite autour de la terre à une altitude telle qu’il en fait le tour en 24 heures. En conséquence, vu de la terre, il ne bouge pas. Il y en a plus de 500 là-haut. On sait comment ça marche.
Dans le monde géocentrique, ils ne tournent donc pas, puisque la terre ne tourne pas non plus. Comment tiennent-ils donc en l’air ? Si je lâche, même de très haut, un objet sans lui donner une vitesse horizontal, il tombe sur la terre. Demandez à Felix Baumgartner. Le géocentrisme répondra que l’effet Lense–Thirring mentionné à la fin du point précédent, fait tenir le satellite en l’air. Mais les 3 objections que nous avions faites sont valables ici aussi. On voit comment le géocentrisme ne rechigne pas à s’enticher des éléments les plus raffinés de la gravitation, tout en lui demandant de faire tout et n’importe quoi, comme vont le montrer les points suivant.
L’univers devrait tourner bien trop vite
Un corps placé à une distance D de la terre devrait parcourir un cercle de périmètre 2piD tous les 24 heures. Sa vitesse le long du cercle serait donc de 2piD/24, en km/h. Quelle doit être la distance D pour que cette vitesse surpasse celle de la lumière ? Environ 4 milliards de kilomètres. Même si ça parait beaucoup, c’est en fait tout petit. Plus petit que le système solaire. Pluton est à 6 (parfois 7) milliards de kilomètres. Et la sonde américaine « New Horizons » va survoler Pluton fin mai 2015. Bref, demain. Si Pluton courrait si vite, ça se saurait[8]. La sonde Voyager 2, lancée en 1977, est en ce moment à 16 milliards de kilomètres et continue d’envoyer des données.
Se pourrait-il que Pluton n’ait pas besoin d’aller plus vite que la lumière, mais que ce soit l’espace lui-même qui l’entraine ? Apres tout, c’est tout à fait ce qui se passe pour les galaxies lointaines. Elles s’éloignent de nous à cause de l’expansion de l’univers, pas de leur mouvement propre. Non. Car ici encore, l’exploration spatiale l’aurait révélé. L’observation aussi, ne serait-ce qu’à cause des formidables effets optiques que cela entrainerait sur les planètes du système solaire.
On peut en fait dire avec certitude qu’avec plus de 100 sondes spatiales[9] qui le parcourent (ou l’ont parcouru), on connait très bien le système solaire. La sonde Philae vient de se poser, après un voyage de 10 ans, sur un caillou de quelques kilomètres de large et distant de 500 millions de kilomètres.
Prétendre que le système solaire est le lieu d’effets aussi étranges,
c’est un peu comme tenter de vous faire croire que le grand canyon du Colorado
se trouve en fait au fond de votre jardin.
Non, rien de bizarre ne se passe dans le système solaire.
La position des étoiles devrait changer sans cesse
Tournons-nous maintenant vers une étoile située comme sur la figure ci-dessous,

On voit bien que pour observer la même étoile à 6 mois d’intervalle, il faut regarder dans une direction différente. Cette variation de l’angle de visée, la « parallaxe », est tout à fait observée et même utilisée pour mesurer les distances soleil-étoiles jusqu’à environ 30 000 années lumières. Le satellite Gaia actuellement en orbite autour du point de Lagrange L2 (voir plus bas) est en train d’en mesurer environ 1 milliard. Il ne s’agit pas d’une exagération. Le nombre de mesures en cours est réellement 1 milliard.
Bien sûr, comme attendu, la parallaxe varie avec une période de 1 an. Qu’en faire dans le modèle géocentrique ? Il faudrait que toutes les étoiles, en plus de tourner autour de nous plus vite que la lumière, et de se rapprocher ou de s’éloigner avec une période de précisément 1 an, oscillent avec la même période afin de mimer les variations de la parallaxe. Ça se complique.
La terre serait vraiment sphérique
La terre est sphérique, ou presque.
A cause de sa rotation, elle est un peu aplatie aux pôles, tel un ballon que l’on ferait rapidement tourner sur lui-même et que la force centrifuge déformerait. Certes, l’effet n’est pas très prononcé car ça ne tourne pas très vite (1 tour en 24 heures), mais il est là. Le diamètre aux pôles est inférieur de 21 km au diamètre à l’équateur.
Le modelé héliocentrique rend parfaitement compte de cela. C’est tout à fait normal. La terre tourne sur elle-même, et la force centrifuge fait le travail. Comment l’expliquer en revanche si la terre est immobile et que c’est tout le reste qui tourne autour ? Comme pour le pendule de Foucault ou les satellites géostationnaires qui ne tombent pas, le géocentriste invétéré invoquera l’effet Lense–Thirring cité plus haut. Et ici encore, il se verra obliger d’emprunter à Einstein les aspects les plus exotiques de sa théorie, tout en la bafouant allègrement avec un soleil qui monte et qui descend pour mimer les saisons.
Comment rendrait-on compte des saisons ?
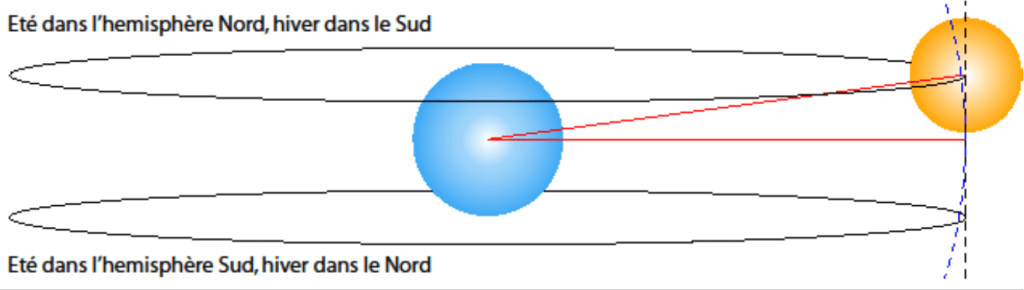
Le soleil n’est pas toujours à la même hauteur dans le ciel. Il monte plus haut en été qu’en hivers. C’est ce qui fait les saisons. Comment en rendre compte s’il tournait autour de la terre ? L’argument est qu’il tournerait parfois dans le plan de l’équateur terrestre, parfois plus haut que ce plan, et parfois plus bas, comme l’illustre la figure ci-dessous. Mais quelle force le ferait bouger ainsi ? Certainement pas la gravité. Pas non plus la force électromagnétique, puisque qu’il est globalement neutre.
De plus, le soleil serait plus proche de nous quand il tourne autour de l’équateur qu’au milieu de l’hiver ou de l’été, comme le montrent les traits rouges sur le dessin. Quand on fait le calcul, on se rend compte que la différence de diamètre apparent se verrait très bien. Et s’il montait et descendait selon l’arc de cercle bleu, au lieu du segment noir en pointillé ? Aucune chance non plus que la gravité ne fasse cela pour nous. Ou alors, il faudrait accepter d’appeler Einstein à l’aide pour expliquer (sans succès) le pendule de Foucault, pour s’en débarrasser au plus vite dès qu’il s’agit de rendre compte des saisons.
La couleur des étoiles devrait changer tout le temps
Imaginons une étoile éloignée du système terre-soleil, comme sur la figure ci-dessous :
On voit bien que selon la position de la terre sur son orbite, la terre se rapproche ou bien s’éloigne de l’étoile. C’est là qu’entre en jeu le radar de votre dernière contravention pour excès de vitesse. Cet appareil est capable de mesurer votre vitesse en observant comment votre voiture lui renvoie un signal lumineux qu’il vient d’émettre. Selon votre vitesse, la fréquence du signal réfléchi change, et permet de savoir si vous allez trop vite. Bref, un objet qui bouge trahit son mouvement par la fréquence de la lumière qu’il émet. Il change de couleur, que nos yeux puissent s’en rendre compte ou pas. En analysant tout cela, on peut savoir si le corps s’éloigne ou se rapproche, et à quelle vitesse. C’est ce qu’on appelle l’effet Doppler.
Bien évidemment, on a fait l’expérience avec les étoiles. Et ça marche très bien. On observe tout à fait comment l’étoile s’éloigne quand la terre va de la position 1 à la 2, puis se rapproche en allant de 2 à 1. Le signal attendu est là, avec un cycle de 1 an[10].
Comment expliquer cela dans un modèle géocentrique ? Il faudrait que toutes les étoiles de l’univers, en plus de tourner autour de nous plus vite que la lumière[11], se rapprochent et s’éloignent avec une période de précisément 1 an. L’amplitude de cette oscillation devrait de surcroît être savamment calculée puisqu’une étoile située dans le plan de l’orbite terrestre, par exemple, ne donne pas le même effet qu’une étoile qui n’y est pas. Une autre option serait qu’elles changent toutes de couleur à l’unisson, de manière à produire l’effet recherché. Enfin, ces acrobaties devraient être savamment dosées pour que le signal des étoiles proches nous parvienne en même temps que celui des lointaines.
Comment expliquerait-on qu’un jour ne fait pas toujours 24 heures ?
L’univers tourne donc autour de nous en 24 heures. Re-admettons. Toujours 24 heures ? Surement pas, car la durée du jour n’est pas toujours de 24 heures. Non, la terre ne tourne pas toujours à la même vitesse. Comme on le voit sur la figure ci-dessous, la durée du jour (LOD = lenght of day) varie de quelques millièmes de seconde selon un patron pas évident du tout, et parfois même assez brusque[12].
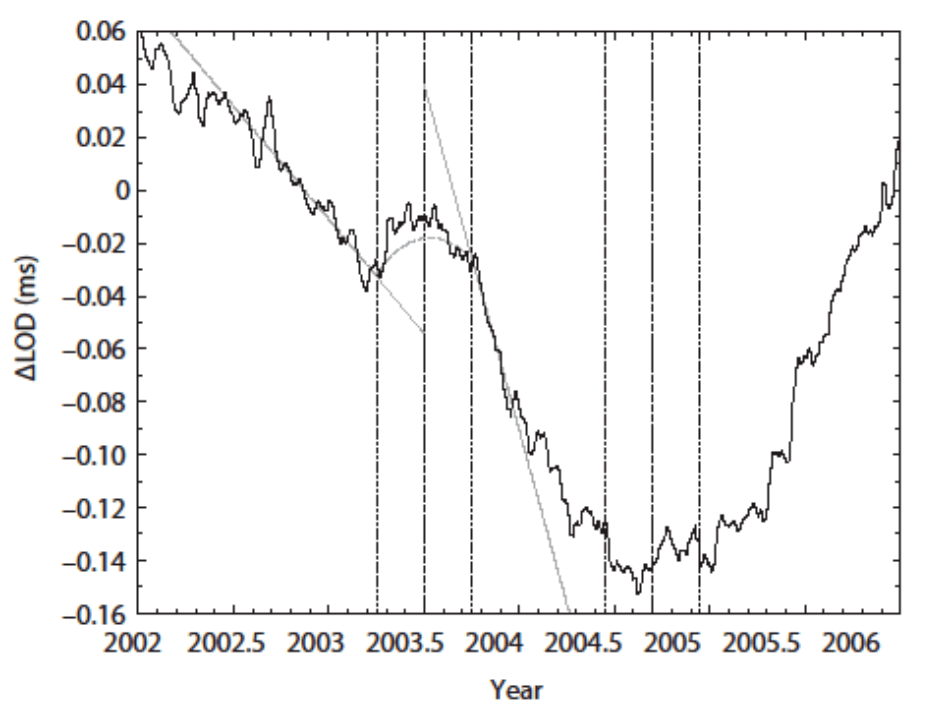
Il faudrait donc qu’en plus de tourner plus vite que la lumière, de se rapprocher et de s’éloigner ou de changer de couleur, les étoiles de l’univers entier ralentissent, puis accélèrent, puis ralentissent, et tout cela dans un synchronisme parfait, pour qu’ici aussi, les hoquets des étoiles proches nous arrivent exactement en même temps que ceux des astres distants de milliers d’années lumières.
Vous avez une aspirine ?
Parce que c’est pas fini.
Le fond diffus cosmologique devrait virevolter
Environ 380 000 ans après le big bang, la matière et la lumière, qui jusque-là dansaient ensemble, se sont séparées. Les photons (grains de lumière) de cette époque se sont libérés, et sont toujours là. On les a détectés. Leur répartition colle à merveille avec les prédictions théoriques. Trois satellites (COBE, WMAP et Planck) ont déjà été mis en orbite[13] pour les étudier en détail. C’est cela, le fond diffus cosmologique (FDC).
On regarde donc dans toutes les directions du ciel et l’on mesure la lumière qui parvient au détecteur, dans la gamme micro-ondes. On trouve ça[14] :
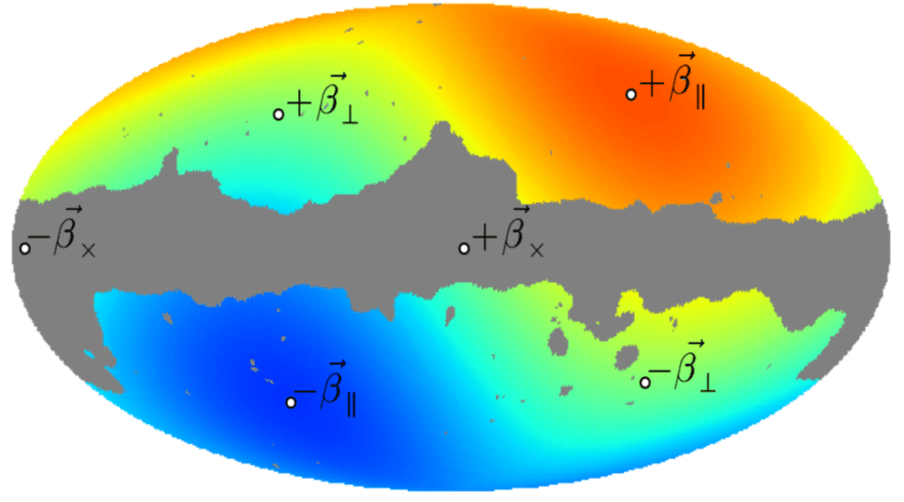
Les couleurs sont forcément fausses car la lumière micro-onde est invisible à l’œil humain. C’est pour cela que vous ne voyez rien de spécial dans votre four du même nom. La bande grise centrale est le lieu de notre galaxie. Sinon, nous avons ici la projection plane d’une image sphérique semblable à certaines cartes du monde.
La première chose qui saute aux yeux est ce dégradé bleu-orange. D’où vient-il ? La lumière arrive dans toutes les directions. Imaginez que vous bougiez par rapport à ce rayonnement. Vous irez à l’encontre de certains photons, et vous en fuirez d’autres. L’effet Doppler évoqué plus haut va donc jouer. La fréquence des photons vers qui vous allez est plus haute. Celle de ceux que vous fuyez et plus basse. Comme le son d’un train qui passe devant vous (aigüe avant, grave après).
En analysant cette image, on peut savoir à quelle vitesse nous nous déplaçons par rapport au rayonnement, et vers où. Pour la vitesse, c’est 369 km/s. Pour la destination, je vous laisse lire le papier cité. Apres avoir « dé-Doppleriser » l’image, ce qui numériquement n’est pas difficile, on peut commencer à analyser le FDC.
Comment rendre compte de cela dans le modèle géocentrique ?
Ce serait donc le FDC qui bouge par rapport aux étoiles ?
Et en plus, puisque l’effet Doppler pointe dans une direction bien précise, le FDC devrait faire un tour complet toutes les 24 heures ? Ça commence à faire beaucoup.
Les points de Lagrange n’existeraient pas
Si l’on considère juste le système terre-soleil, il existe 5 points privilégiés dans l’espace, baptisés L1, L2, L3, L4 et L5, où un corps peut rester au repos aussi longtemps qu’il le veut[15]. Ces points tournent avec la terre, et n’existent qu’en vertu de la force centripète qui s’exerce sur un corps en rotation autour du soleil. En ce moment même, 6 sondes tournent autour de L1[16]. 5 autour de L2. Plusieurs autres missions sont prévues pour L1 et L2. Bref, on sait comment ça marche. On est allé vérifier sur place. Mais aucune chance que ça fonctionne si on ôte la force centripète fruit de la rotation autour du soleil.
Juste un petit dernier pour la route : le bruit court que les agences spatiales du monde entier sauraient la vérité et utiliseraient le modèle géocentrique pour calculer les trajectoires de leurs fusées. Il faudra donc se demander pourquoi elles s’évertuent à lancer leurs jouets depuis une base la plus proche possible de l’équateur terrestre : Cap Canaveral pour les USA, Kourou en Guyane pour l’Europe, Baïkonour pour l’ex URSS. Quant aux Chinois, ils sont en train d’en construire une dans l’île de Hainan, on ne peut plus au sud de leur territoire. Pourquoi, donc ? Parce la rotation de la terre produit une force centripète qui aide une fusée à décoller. Et cet effet est maximum précisément à l’équateur.
La liste est longue[17], et je propose qu’on en reste là.
Retour sur terre
Heureusement pour nous, la nature réelle est bien plus simple que celle du modèle géocentrique. Des milliards d’observations deviennent des banalités dans l’héliocentrisme tandis qu’elles sont inexplicables pour le géocentrisme. Dans le meilleur des cas, elles nécessiteront des milliards d’hypothèses différentes et complément ad-hoc.
Notons que le mot « milliard » ne résulte pas d’une hyperbole. Nous avons des preuves observationnelles que l’univers contient plus de 100 milliards de galaxies. Comptez quelques centaines de milliards d’étoiles par galaxie. Ça commence à faire du monde que le modèle géocentrique doit faire bouger dans tous les sens, et en dépit des lois de la physique les plus éprouvées.
Revenons donc sur terre. Un référentiel inertiel est un référentiel dans lequel la loi de Newton énoncée au début de l’article est valable. Un référentiel dans lequel on observe qu’un objet qui se déplace en ligne droite continue de le faire tant qu’on ne l’embête pas. Un référentiel dans lequel les pendules ne tournent pas. Tous les référentiels inertiels se valent. Notons que si tous « se valent » du point de vue des lois de Newton, tous ne sont pas « zéro Doppler » vis-à-vis du FDC. Il se pourrait bien qu’on tienne là LE référentiel des référentiels[18].
Concrètement, la meilleure manière de trouver un référentiel inertiel est de se repérer par rapport à des étoiles lointaines. Dans un tel référentiel donc, attachez deux sphères avec une corde, pour mimer la gravitation, puis faites-les tourner l’une autour de l’autre. Vous les verrez tourner autour du centre de gravité de l’ensemble. Pour le système terre-soleil, le soleil est si lourd que le centre de gravité est à 442 km de son centre. Et comme c’est une sphère d’environ 1,4 millions de km de diamètre, le soleil tourne autour d’un point qui coïncide presque avec son centre[19]. Et la terre, elle tourne autour du même point, c’est-à-dire autour du soleil.
 Et quand on regarde en l’air et qu’on a la chance de surprendre un système planétaire en formation, on voit ça :
Et quand on regarde en l’air et qu’on a la chance de surprendre un système planétaire en formation, on voit ça :
Ce n’est pas une simulation d’ordinateur. Ce n’est pas un dessin. C’est une photo[20].
Le lourd, l’étoile, est au milieu. Le reste, poussières, roches et planètes en formation, tourne autour. Quant au géocentrisme militant, je crains fort qu’il n’illustre à merveille les propos d’Ecclésiaste 7:29,
« Dieu a fait les hommes droits mais eux, ils ont cherché beaucoup de complications » (Semeur).
Voir aussi sur le blog : https://scienceetfoi.com/est-il-encore-possible-de-croire-que-la-terre-est-fixe-et-que-le-soleil-tourne-autour/
Notes
[1] Qui n’est en fait qu’une pseudo-force qu’il convient d’ajouter à la loi de Newton pour décrire correctement le mouvement du pendule dans le référentiel lié à la terre.
[2] Il s’agit en fait de la définition même d’un tel référentiel. Un référentiel inertiel est, par définition, un référentiel où la loi de Newton fonctionne. Voir par exemple la première page de Landau & Lifchitz, Physique Théorique : Théorie des Champs
[3] Par rapport à quoi? Mais laissons cela de côté pour le moment.
[4] Certes, le satellite n’est pas dans la terre. Il tourne autour. Mais la relativité générale prédit le même effet pour un objet à côté d’une sphère en rotation.
[5] Voir http://en.wikipedia.org/wiki/Mach’s_principle
[6] On en connait à ce jour plus de 1 000, chacune en orbite autour de leur propre soleil. Voir http://fr.wikipedia.org/wiki/Exoplanète.
[7] On n’a toujours pas dit par rapport à quoi…
[8] Passons sur le fait qu’une étoile située par exemple à 100 années lumières devrait tourner à 229 000 fois la vitesse de la lumière. Je vous laisse calculer la vitesse de la galaxie d’Andromède, notre voisine située à 2,5 millions d’années lumières.
[9] Voir http://fr.wikipedia.org/wiki/Liste_des_sondes_spatiales. Il y en bien plus, mais j’ai arrêté de compter à 100.
[10] Voir par exemple, Koupelis, In Quest of the Solar System, Jones & Bartlett Publishers, 2010, p. 118.
[11] Aucune étoile ne se trouve à moins de 4 milliards de kilomètres. Loin s’est faut. La plus proche, Alpha de Centaure, est à 4,37 années lumières (41 000 milliards de kilomètres). Elle tourne à presque 10 000 fois la vitesse de la lumière dans le modèle géocentrique.
[12] La chose est reliée à la dynamique interne de la terre. Voir Holme & Viron, Characterization and implications of intradecadal variations in length of day, Nature 499, 202–204 (2013). Je montre la figure 2.
[13] COBE autour de la terre. Les deux autres autour du point de Lagrange L2 que nous venons d’évoquer.
[14] C’est la figure 2 de cet article: Planck Collaboration, Planck 2013 results. XXVII. Doppler boosting of the CMB: Eppur si muove, Astronomy & Astrophysics 571, A27 (2014). En ligne gratuitement ici: http://arxiv.org/abs/1303.5087.
[15] Ou presque, à cause de sombres histoires de stabilité. Mais oublions ça.
[16] Voir http://en.wikipedia.org/wiki/Lagrangian_point.
[17] Les pulsars, par exemple, fournissent pas mal de test. Voir Lyne & Graham-Smith, Pulsar Astronomy, Cambridge University Press, 2012.
[18] Le seul, peut-être, qui permettrait de donner un sens au mot « fixe » sans devoir regarder aucune étoile. Notons cependant que même si nous n’observions aucun effet Doppler sur le FDC, ça ne voudrait rien dire. C’est exactement ce qui se passe pour les milliards d’étoiles de l’univers qui se déplacent à 369 km/s dans la bonne direction (par rapport à nous).
[19] J’oublie ici les autres planètes, qui compliquent un peu les choses. Voir http://fr.wikipedia.org/wiki/Coordonnées_barycentriques_(astronomie).
[20] Pour plus de détails, http://www.eso.org/public/images/eso1436a/